X X X X Is Equal To 4x Graph - A Look At Math And Its Uses
Have you ever stopped to think about how simple math ideas can actually open up a whole world of possibilities? There is, you know, this rather straightforward mathematical expression, "x plus x plus x plus x," that simply means the same thing as "four times x." It seems quite basic at first glance, but what it represents, especially when you picture it, holds quite a bit of importance for how we look at numbers and shapes. This idea, really, is a core piece of what makes up algebra, showing us how we can take symbols and make them simpler.
This particular mathematical statement, "x + x + x + x is equal to 4x," provides a very clear example of how algebraic rules work. It shows how letters, or variables, can be made less complicated and changed around, forming the very building blocks of number work. We often use these kinds of simple changes to figure out much bigger problems, and it all starts with recognizing patterns like this one. So, in a way, this basic idea is a tiny window into the bigger picture of how math helps us organize and make sense of information.
Today, we're going to take a closer look at this idea and its picture form, what we call a graph. We'll consider what it means when we put it on a coordinate plane, how it helps us see math, and how we can use tools to draw it out. It’s almost like seeing the numbers come to life, allowing us to grasp connections that might be harder to spot just by looking at the symbols alone. This kind of visual aid, you see, makes math much more approachable for many people.
Table of Contents
- What Does "x + x + x + x = 4x" Really Mean?
- Why Do We Picture Math - The "x x x x is equal to 4x" Graph?
- How Do Online Calculators Help Us Picture the "x x x x is equal to 4x" Graph?
- Can We Solve for "x" in "x x x x is equal to 4x"?
- What About Other Math Operations?
- Are There More Dimensions for the "x x x x is equal to 4x" Graph?
- Who Finds the "x x x x is equal to 4x" Graph Useful?
- What Makes This Simple Equation So Important?
What Does "x + x + x + x = 4x" Really Mean?
Let's consider what the expression "x + x + x + x is equal to 4x" truly represents. At its heart, this mathematical statement is about combining things that are the same. Imagine, if you will, that 'x' stands for something, perhaps a single apple. If you have one apple, and then another apple, and then another, and one more apple, you would end up with four apples, wouldn't you? That's what this equation is showing us, very simply put. It's a way of saying that adding the same thing to itself a certain number of times is the same as multiplying that thing by the number of times it appears. So, in some respects, it's a fundamental truth of how numbers work.
The essence of "x + x + x + x is equal to 4x" really comes down to a basic rule of arithmetic called multiplication. Multiplication is, after all, just a quick way to do repeated addition. So, when you see 'x' written out four separate times and added together, it's just a longer way of writing '4' multiplied by 'x'. The 'x' itself is a variable, a placeholder for any number you might want to put in there. It could be 1, or 5, or 100, or even a fraction; the rule still holds. This kind of simplification, you see, makes working with equations much tidier.
Breaking down "x + x + x + x is equal to 4x" shows us how we take a collection of identical items and express them in a more compact form. This principle is a cornerstone of algebra, which is a branch of mathematics that uses letters and symbols to represent numbers and quantities in formulas and equations. It helps us solve problems where we don't know the exact number right away, allowing us to work with general ideas. This simple idea, you know, is the very beginning of understanding how to work with unknown values in math.
Why Do We Picture Math - The "x x x x is equal to 4x" Graph?
Why do we bother drawing pictures of mathematical statements? Well, picturing math, especially something like the "x + x + x + x is equal to 4x" graph, gives us a different way to grasp what's going on. When we put an equation onto a visual display, it turns abstract numbers and symbols into something we can actually see and point to. A graph, in this case, is like a map for our equation, showing us all the possible pairs of numbers that make the statement true. It's really quite a neat way to make sense of things.
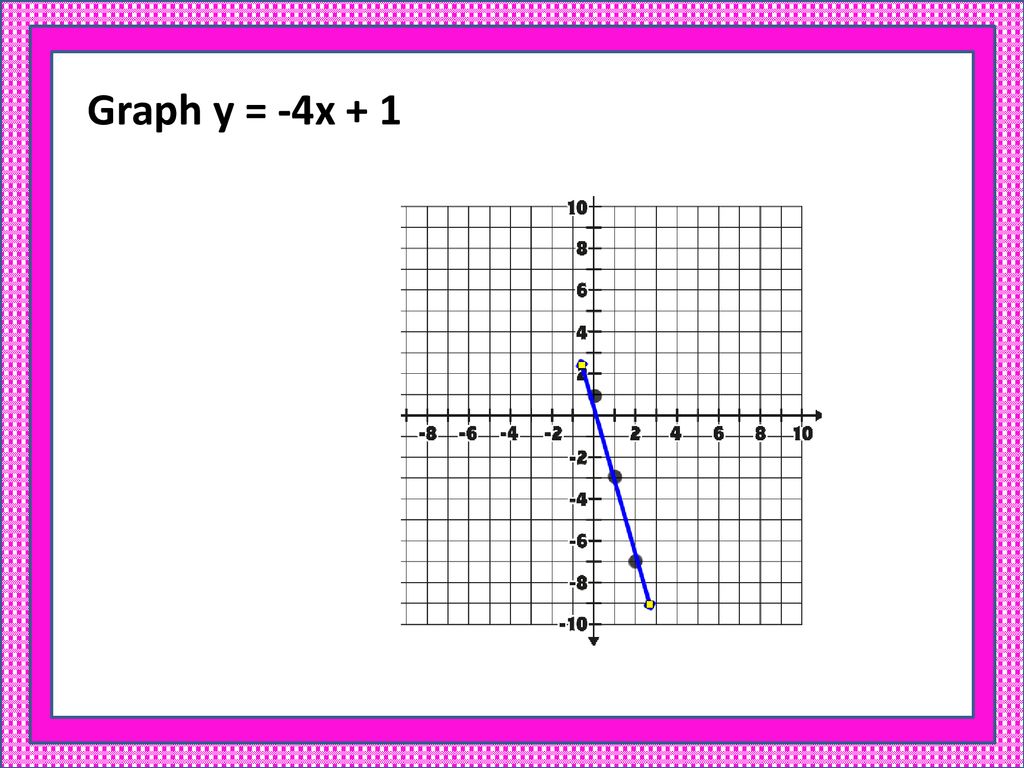
For the specific statement "x + x + x + x is equal to 4x," when we draw its graph, we are essentially drawing the line for the equation 'y = 4x'. Here, 'y' would represent the outcome of '4x' for any given 'x'. This line shows us that for every single step 'x' takes along the horizontal line, the 'y' value goes up four times as much on the vertical line. It’s a straight line, passing right through the point where both 'x' and 'y' are zero. This visual representation, you know, makes the relationship between 'x' and 'y' very clear and immediate.
Drawing the "x x x x is equal to 4x" graph helps us to see the pattern of growth or change that the equation describes. It allows us to pick any 'x' value and then look directly at the graph to find its corresponding 'y' value, or vice versa. This visual aid is particularly helpful for people who learn better by seeing things rather than just reading symbols. It's a way of making the numbers less intimidating and more approachable, giving us, you know, a different way to think about how things connect.
How Do Online Calculators Help Us Picture the "x x x x is equal to 4x" Graph?
Online graphing calculators, like those from GeoGebra or Desmos, make drawing the "x x x x is equal to 4x" graph incredibly easy. These tools are built to help people explore math concepts visually. You simply type in the equation, perhaps "y = 4x," and the calculator instantly draws the line for you. It's like having a personal math assistant that does the drawing part so you can focus on what the picture means. This kind of tool, you see, takes away a lot of the manual work and lets you experiment.
What makes these tools so useful for seeing the "x x x x is equal to 4x" graph is their interactive nature. You can, for example, add sliders to change numbers in an equation and watch how the line moves. You can plot specific points to see if they land on the line, or you can even animate graphs to watch changes over time. Symbolab, another type of online helper, does more than just draw; it often shows you the step-by-step process of how to get to the solution or how to draw the graph. This showing of steps, you know, can be very helpful for learning.
These graphing tools are truly a wonderful resource for anyone trying to get a grasp on mathematical ideas. They allow you to graph functions, plot specific locations, see algebraic equations, add movable parts, and even make graphs move. Symbolab, in particular, is a step-by-step helper for many math problems, from basic number work to more advanced topics. It shows you the solution, the picture, and a detailed explanation of how to get there. It's really quite a straightforward way to learn by doing, and seeing the results right away, which, you know, makes a big difference.
Can We Solve for "x" in "x x x x is equal to 4x"?
The question of whether we can "solve for x" in the equation "x + x + x + x is equal to 4x" is an interesting one. When we talk about solving for 'x', we usually mean finding a specific number that 'x' must be to make the equation true. However, in this particular equation, "x + x + x + x = 4x," the statement is always true, no matter what number 'x' stands for. If 'x' is 5, then 5 + 5 + 5 + 5 equals 20, and 4 times 5 also equals 20. If 'x' is 0, then 0 + 0 + 0 + 0 equals 0, and 4 times 0 also equals 0. So, there isn't one single answer for 'x'. It's, you know, a general truth.
This kind of equation, where both sides are always equal regardless of the value of the variable, is sometimes called an identity. It's not a problem to be solved for a single numerical answer, but rather a statement of equivalence. It shows that the expression on the left side is simply a different way of writing the expression on the right side. A calculator that helps you solve for 'x' typically looks for a single numerical answer, but for an identity like this, it would confirm that the equation holds true for any value of 'x'. This is, you know, a different kind of mathematical truth.
So, while you can put this into a "solve for x" calculator, it won't give you a number like 'x = 7'. Instead, it would essentially confirm that the equation is always true, or it might show you the steps to simplify the left side to match the right side. It's a fundamental principle of algebra, showing how variables can be simplified and changed, forming the basic structure of algebraic expressions. It’s really quite a basic idea, but one that underpins a lot of what we do in math, you know, when we are trying to make things simpler.
What About Other Math Operations?
When we think about "x + x + x + x is equal to 4x," we are focusing on addition and multiplication. But what about other mathematical operations? Algebra, as a section of mathematics, lets you do much more than just combine like terms. It allows you to expand expressions, which means taking something compact and writing it out in a longer form, like changing '4x' back into 'x + x + x + x'. It also lets you factor expressions, which is the opposite process: taking a longer expression and finding common parts to write it in a shorter, multiplied form. So, in a way, it's about seeing different patterns.
For instance, if you had an expression like '2x + 6', you could factor it to '2(x + 3)'. This shows that both terms have a common factor of 2. These operations are crucial for working with more complex equations and expressions, allowing us to rearrange them to find answers or to see relationships more clearly. Online tools often have sections dedicated to these kinds of operations, helping you to see how to expand, factor, or simplify various algebraic statements. It's, you know, a very useful set of skills to have.
Beyond basic simplification, algebra also deals with things like derivatives and limits, which are concepts found in calculus. While "x + x + x + x is equal to 4x" is a basic algebraic identity, the principles of working with variables and expressions extend to these higher-level ideas. For example, you can enter any function to find its derivative, which tells you about its rate of change, or enter a limit you want to find, which helps you understand what a function approaches. These tools are built to help you see the solution, the steps, and the graph for these more advanced concepts too. It’s really quite amazing what these tools can do, allowing us to explore, you know, so many different aspects of numbers.
Are There More Dimensions for the "x x x x is equal to 4x" Graph?
When we talk about the "x x x x is equal to 4x" graph, we usually picture it in two dimensions: the 'x' axis going sideways and the 'y' axis going up and down. This creates a flat surface, like a piece of paper, where we draw our line. But have you ever felt like two dimensions isn't quite enough to picture some ideas? It’s true that many things in our everyday experience exist in three dimensions, having length, width, and depth. So, can we picture this simple equation in more dimensions?
While the equation "y = 4x" itself is a two-dimensional relationship, the concept of variables and graphing can certainly extend into higher dimensions. For instance, tools like the Desmos 3D calculator let you explore curves, surfaces, and points in all three dimensions. If we were to introduce a third variable, say 'z', our equation would change, perhaps to 'z = 4x', or 'z = 4y', or even 'z = 4x + 4y'. Then, instead of a line, we would see a flat surface in three-dimensional space. This allows us to see, you know, how math can describe our physical world.
Breaking down "x + x + x + x is equal to 4x" reveals a fundamental algebraic idea that can be built upon. While its direct graphical representation is a simple line in two dimensions, the principles it embodies are the foundation for working with more complex equations and visual representations in higher dimensions. It just goes to show that even the simplest mathematical truths can be expanded and applied in many different ways, allowing us, you know, to picture things that are far more intricate.
Who Finds the "x x x x is equal to 4x" Graph Useful?
So, who actually finds the "x x x x is equal to 4x" graph, and the idea behind it, useful? Well, it's trusted by millions of teachers and students worldwide, which tells you quite a bit. For students just starting out with algebra, this equation is often one of the very first examples they encounter. It helps them grasp the concept of variables, how to combine like terms, and how to represent an equation visually. It's a foundational piece of learning, really, that helps build confidence in working with numbers and symbols. It’s, you know, a stepping stone to more advanced topics.
Teachers use this example because it is a basic yet profound illustration of algebraic principles at work. It showcases how variables can be simplified and changed, forming the basic structure of algebraic expressions. It's a clear, straightforward way to introduce the idea of a linear relationship – where one quantity changes directly in proportion to another. This simple relationship, you see, is found everywhere in the real world, from calculating distances to understanding how money grows. It’s, in a way, a universal concept.
Beyond the classroom, anyone who uses data or needs to understand proportional relationships might find the underlying idea helpful, even if they don't explicitly think of "x + x + x + x = 4x." For example, if you're tracking how much you earn for each hour you work, and your hourly rate is constant, that's a "y = 4x" type of relationship if your rate was 4 dollars an hour. It’s a way of thinking about how things scale. So, while the equation itself is simple, the principle it teaches is widely applicable, you know, across many different fields.
What Makes This Simple Equation So Important?
The equation "x + x + x + x is equal to 4x," while it might seem incredibly simple at first glance, carries a lot of importance in the world of mathematics. Its significance doesn't come from its difficulty, but from its fundamental nature. It serves as a clear, straightforward example of how repeated addition can be expressed as multiplication, a concept that is absolutely basic to all arithmetic and algebra. It’s, you know, a building block for everything else.
At the heart of this mathematical idea lies a foundation that warrants careful examination. Breaking down "x + x + x + x is equal to 4x" reveals a simple truth about combining identical items. This truth allows us to simplify expressions, making complex problems easier to handle. It teaches us about variables, coefficients, and the very structure of algebraic statements. This foundational understanding is what allows us to then move on to more complicated equations, graphs, and mathematical models. It’s, you see, the very start of a long path of discovery.
This basic equation is like a first lesson in mathematical shorthand. It shows us that there are more efficient ways to write and think about numbers. It also introduces the idea that an equation can represent a relationship that holds true for many different numbers, not just one specific answer. This concept of identity is powerful, paving the way for understanding more abstract mathematical ideas and how they apply to the world around us. It’s, you know, a very small piece of math that teaches a very big lesson.
Using Slope Intercept Form to Graph - ppt download

Graph the linear function p(x ) = 4x - brainly.com
Types Of Graphs Functions