How To Convert Degrees To Radians - A Simple Guide
Have you ever looked at a circle and wondered about the different ways we talk about its turns? It's kind of fascinating, isn't it? We usually think about angles in terms of degrees, like a quarter turn being ninety degrees, or a full spin being three hundred and sixty degrees. This way of measuring feels very familiar to most of us, something we pick up quite early on. It helps us describe everything from the tilt of a ramp to the opening of a door, which is pretty neat.
But then, there's another way to measure these turns, a different language for angles, if you will. This other way uses something called "radians." Now, for some folks, radians might sound a bit more involved, or perhaps a little like something you only see in a textbook. However, they are actually a very natural way to measure angles, especially when you are dealing with circles and things that move in a circular path. It's almost as if they speak the circle's own language, which is rather interesting, you know?
So, why do we have two ways to measure the same thing, and how do we switch between them? Well, it turns out that both degrees and radians have their own special places where they really shine. Sometimes, one is just a better fit for what you are trying to describe or calculate. This piece is all about making that switch from degrees to radians feel really simple and straightforward. We'll go over how to convert degrees to radians, step by step, using some clear examples from "My text" to show you exactly how it works. It's actually pretty easy once you get the hang of it, and we will break it all down for you.
Table of Contents
- What are Degrees and Radians, Anyway?
- Why Do We Need to Convert How to Convert Degrees to Radians?
- The Simple Idea Behind How to Convert Degrees to Radians
- What's the Main Tool for How to Convert Degrees to Radians?
- Putting the How to Convert Degrees to Radians Rule to Work
- Can We Change Radians Back to Degrees?
- More Situations for How to Convert Degrees to Radians
- What are the Key Bits for How to Convert Degrees to Radians?
What are Degrees and Radians, Anyway?
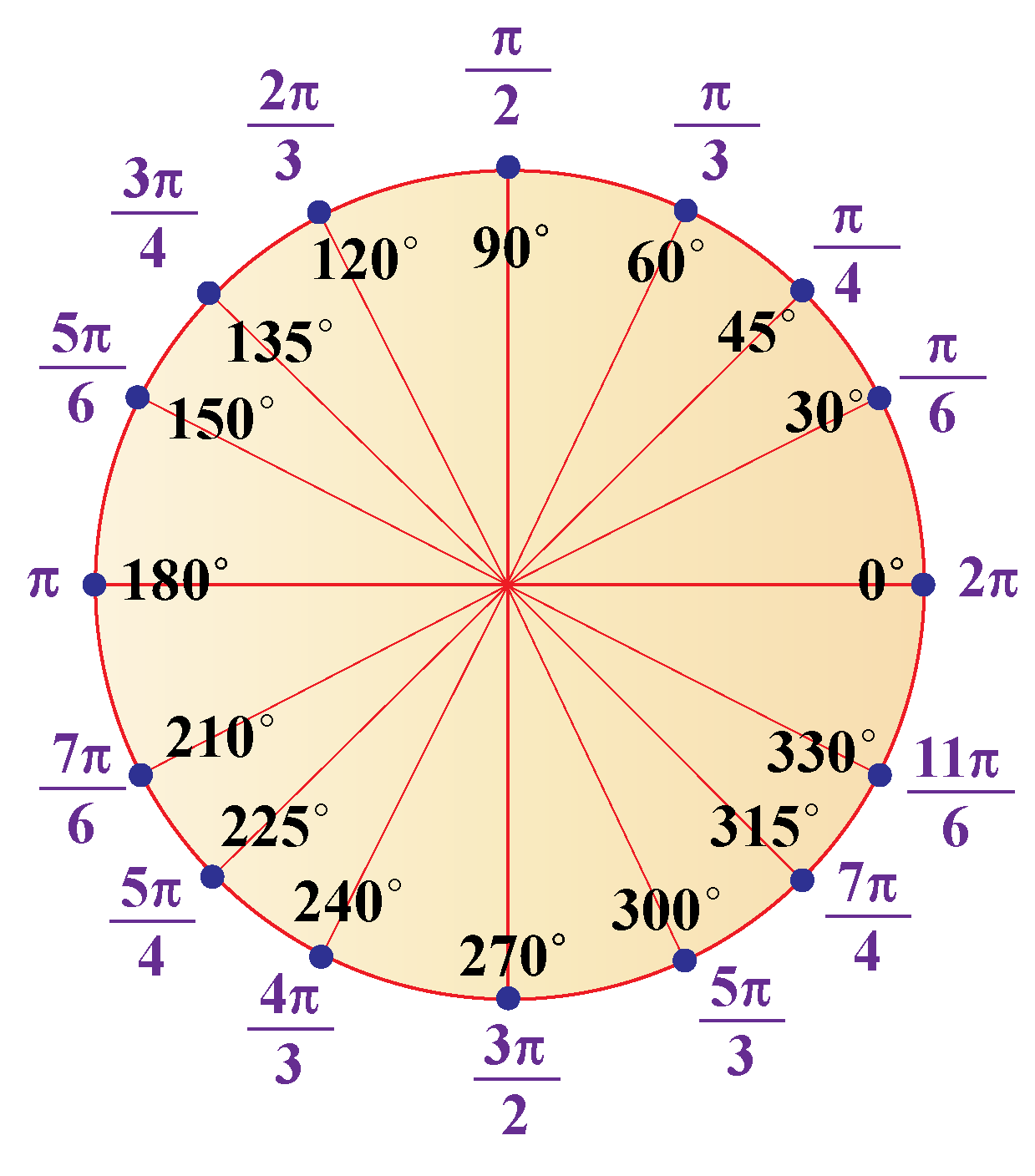
When we talk about angles, we are really just talking about how much "turn" there is between two lines or how much of a circle we have gone around. Degrees are what most of us grew up with. Think of a full circle as having three hundred and sixty individual little steps, each one a "degree." So, if you turn a quarter of the way around, that is ninety of those steps, or ninety degrees. If you turn halfway, it's one hundred and eighty degrees, and a complete spin brings you back to three hundred and sixty degrees. It's a system that feels very natural and easy to picture, you know?
Radians, on the other hand, are a little different. They are based on the circle's own measurements, specifically its radius. Imagine you have a circle, and you take a piece of string the same length as the circle's radius. If you then lay that string along the edge of the circle, the angle formed by drawing lines from the center to the two ends of that string is one radian. It's a very natural way to measure angles because it ties directly into the geometry of the circle itself. So, a full circle, which is three hundred and sixty degrees, actually works out to be about six point two eight radians, or, more precisely, two times pi radians. This connection between the circle's radius and its edge makes radians particularly useful in higher-level math and science, especially when things are moving in circles, or if you're dealing with waves and oscillations, which is quite interesting.
Why Do We Need to Convert How to Convert Degrees to Radians?
You might be wondering why we even bother with two different ways to measure angles. It seems like it could make things a bit more complicated, doesn't it? Well, the truth is, both degrees and radians have their own special uses where they just make more sense. Degrees are fantastic for everyday things and for drawing. When you tell someone to turn ninety degrees, they have a clear picture in their head. It's a very intuitive way to think about turns and rotations. So, for things like carpentry, navigation, or even just giving directions, degrees are usually the go-to choice. They are, for many people, simply easier to visualize and work with in practical situations, which is a big plus.
However, when you step into the world of higher mathematics, physics, and engineering, radians often become the preferred unit. Why? Because many mathematical formulas that involve angles, especially those related to trigonometry, calculus, and circular motion, become much simpler and more elegant when angles are expressed in radians. For instance, the rate of change of a sine wave, when the angle is in radians, is just the cosine wave itself. If you used degrees, there would be an extra conversion factor cluttering up the equation, which is not ideal. So, radians help keep those complex equations neat and tidy. It's kind of like how some tools are just better suited for certain jobs. So, knowing how to convert degrees to radians becomes a really handy skill when you are dealing with these kinds of subjects, as it helps you speak the language of the formulas directly.
The Simple Idea Behind How to Convert Degrees to Radians
The core idea behind changing degrees into radians, or the other way around, comes from one very important piece of information: a full circle. We all know that a full turn around a circle is three hundred and sixty degrees. But, as we talked about, a full turn can also be described using radians, and that amount is exactly two times pi radians. So, basically, three hundred and sixty degrees is the same as two pi radians. This is our fundamental connection, our bridge between the two ways of measuring. It's the key relationship that allows us to move from one system to the other, which is pretty cool, if you think about it.
Since three hundred and sixty degrees equals two pi radians, we can simplify that relationship a little bit. If you divide both sides by two, you find that one hundred and eighty degrees is the same as just one pi radian. This simpler relationship, one hundred and eighty degrees equals pi radians, is often the one people remember and use most often. It is, in a way, the more convenient number to work with for these kinds of changes. This bit of information forms the basis for our conversion rule. So, when you want to figure out how to convert degrees to radians, you will always be thinking about this special link between one hundred and eighty degrees and pi. It's actually quite straightforward once you have that basic idea down, and it helps make all the calculations much clearer.
What's the Main Tool for How to Convert Degrees to Radians?
The primary tool, or the main rule, for changing a degree measurement into a radian measurement is a simple formula. It takes that core idea we just talked about – that one hundred and eighty degrees is the same as pi radians – and puts it into a usable format. The rule basically says that if you have an angle given in degrees, and you want to know what it is in radians, you just need to multiply that degree number by a special fraction. This fraction is pi divided by one hundred and eighty. So, the formula looks like this: Angle in radians equals Angle in degrees multiplied by (pi / 180).
Let's think about why this fraction works. When you multiply by (pi / 180), you are essentially setting up a proportion. You are saying, "If one hundred and eighty degrees is equivalent to pi radians, then my specific degree amount must be equivalent to some specific radian amount." The one hundred and eighty in the bottom part of the fraction helps to "cancel out" the degree unit, leaving you with radians. It's a bit like changing units in other areas, such as converting inches to centimeters. You use a conversion factor to make the change. This specific fraction, pi over one hundred and eighty, acts as our special conversion factor for how to convert degrees to radians. It's really quite a neat trick for making the change, and once you use it a few times, it becomes very familiar, you know?
Putting the How to Convert Degrees to Radians Rule to Work
Let's try an example to see this rule in action. Imagine you have an angle of ninety degrees, and you want to express it in radians. Based on "My text," we know ninety degrees is the angle we are starting with. So, we take our rule: Angle in radian equals angle in degree multiplied by (pi / 180). We put ninety in place of "angle in degree." This gives us: ninety multiplied by (pi / 180). Now, we just do the math. Ninety divided by one hundred and eighty is one-half. So, ninety times (pi / 180) becomes (1/2) times pi, which we write as pi over two. Therefore, ninety degrees is equal to pi over two in radians. It's actually quite simple when you break it down, isn't it?
Let's try another one, also mentioned in "My text": one hundred and thirty-five degrees. We follow the same steps. We take one hundred and thirty-five and multiply it by our special fraction, (pi / 180). So, we have one hundred and thirty-five multiplied by (pi / 180). To simplify this, you can find a common number that divides both one hundred and thirty-five and one hundred and eighty. Both numbers can be divided by forty-five. One hundred and thirty-five divided by forty-five is three, and one hundred and eighty divided by forty-five is four. So, the fraction one hundred and thirty-five over one hundred and eighty simplifies to three over four. This means one hundred and thirty-five degrees is equal to three pi over four in radians. You see, the process for how to convert degrees to radians is always the same: multiply by pi over one hundred and eighty, and then simplify the fraction as much as you can. It's a pretty consistent approach, which makes it easier to remember.
Can We Change Radians Back to Degrees?
Yes, absolutely! The great thing about this relationship between degrees and radians is that it works both ways. If you can go from degrees to radians, you can certainly go from radians back to degrees. The key is to just flip our special fraction. Remember, to go from degrees to radians, we multiplied by (pi / 180). So, to go from radians to degrees, we do the opposite: we multiply by (180 / pi). It's really that straightforward, you know? This reverse rule uses the same core idea that one hundred and eighty degrees is the same as pi radians, just applied in the opposite direction. It's kind of like having a two-way street for angle measurements, which is pretty convenient.
"My text" gives an example of converting four point zero radians into degrees. So, we take four point zero and multiply it by our new special fraction, (180 / pi). This would give us (four point zero multiplied by one hundred and eighty) all divided by pi. When you do the multiplication, four point zero times one hundred and eighty is seven hundred and twenty. So, the result is seven hundred and twenty divided by pi degrees. If you need a numerical answer, you would then use the approximate value of pi (about three point one four one five nine) to get a decimal number. This shows that the process for how to convert degrees to radians, and vice versa, is very symmetrical. You just need to pick the correct version of the conversion factor depending on which way you are going, which is actually quite simple to figure out.
More Situations for How to Convert Degrees to Radians
Let's look at another common angle, like forty-five degrees, and see how it converts to radians. "My text" also mentions this one. Using our standard method for how to convert degrees to radians, we take forty-five degrees and multiply it by (pi / 180). So, we have forty-five multiplied by (pi / 180). Now, we need to simplify the fraction forty-five over one hundred and eighty. We know that forty-five goes into one hundred and eighty exactly four times. So, forty-five divided by forty-five is one, and one hundred and eighty divided by forty-five is four. This means forty-five degrees is equal to pi over four in radians. It's a very common angle to convert, and you will see it pop up quite a bit in different problems, which is good to know.
The whole point of these conversions is that angles can be represented in two different ways, and sometimes one way is more helpful than the other. Whether we are talking about the angle between two lines or the total turn of a circle, both degrees and radians give us a way to describe that amount of rotation. The idea that a total circle is three hundred and sixty degrees, or that it is also two pi radians, is the cornerstone of all these changes. It's the fixed relationship that allows us to always move smoothly between the two systems. So, whenever you are faced with a problem involving angles, you can always choose the unit that makes the most sense for what you are trying to accomplish, and then use these straightforward rules to switch if you need to. It really gives you a lot of flexibility in how you approach these kinds of tasks, which is very useful, in a way.
What are the Key Bits for How to Convert Degrees to Radians?
When you are working with angles and need to switch between degrees and radians, there are a few important things to keep in mind. First, always remember that the total angle of a circle is our main reference point. That is three hundred and sixty degrees, which is the same as two pi radians. This fundamental connection is what everything else builds upon. So, if you can keep that simple fact in your head, you are already halfway there, you know? It's the anchor for all your conversions, which is pretty helpful.
Second, when you are converting degrees to radians, you will always be multiplying your degree amount by that specific fraction: pi over one hundred and eighty. And if you are going the other way, from radians to degrees, you just flip that fraction and multiply by one hundred and eighty over pi. It's a pretty neat and tidy system, actually. "My text" mentions that the key numbers we use for this are two pi and three hundred and sixty degrees. These numbers are what help us set up the correct proportion every single time. So, choosing the right form of the conversion factor is really about knowing which way you are going with your angle measurement. It’s about picking the right tool for the job, and with these simple rules, you can handle pretty much any angle conversion you come across, which is very empowering.
This article has walked through the process of changing angle measurements from degrees to radians, and even touched on how to go the other way. We started by understanding what degrees and radians are, then explored why we use both systems. The core idea of three hundred and sixty degrees equaling two pi radians was introduced as the foundation for conversion. We then looked at the main rule for how to convert degrees to radians, which involves multiplying by pi over one hundred and eighty. Several examples, including converting ninety degrees, one hundred and thirty-five degrees, and forty-five degrees to radians, were explained step by step. The article also covered how to change radians back to degrees by using the inverse conversion factor. Finally, it highlighted the important points to remember when dealing with these angle transformations.

How to Convert Degrees to Radians: 5 Steps (with Pictures)

How to Convert Degrees to Radians: 5 Steps (with Pictures)
Converting degrees to radians - Cuemath