Variance Formula
Understanding the Variance Formula - A Simple Guide
When you look at a collection of numbers, it's often helpful to know how much those numbers spread out from each other. Think about a group of friends and their heights; some might be very tall, others quite short, and many somewhere in the middle. Knowing how much those heights differ gives you a good sense of the group. This idea of spread, or how scattered numbers are, is really what we are getting at with something called variance. It helps us see how individual pieces of information move away from a central point, which is typically the average value of everything. So, it's almost like a measure of how much variety there is in a set of figures.
Getting a handle on how much numbers vary is a big deal in many different areas, from understanding sports scores to looking at financial trends or even just seeing how consistent a process might be. The way we measure this spread is through something called the variance formula. It gives us a single number that tells a story about the distribution of data points. A smaller number means the data points are quite close together, while a bigger number suggests they are quite spread out. This numerical value helps us gauge how widely individual items in a group might differ from the usual.
Learning about the variance formula does not need to be a difficult task. We can certainly break it down into smaller, more manageable pieces. There are, as a matter of fact, a few ways to figure out an estimate for the spread of an entire group, and we will talk about these differences as we go along. Whether you are curious about how to figure this out by hand or if you just want to get a general idea of what the number means, we can certainly make sense of it together. You know, it's really about getting a clearer picture of information sets.
Table of Contents
- What is Variance and Why Do We Care?
- How Do We Think About the Variance Formula?
- Different Ways to Calculate the Variance Formula
- How Do You Work Out the Variance Formula by Hand?
- What is the Connection Between Variance and Standard Deviation?
- Using a Tool for the Variance Formula
- What Does a Number From the Variance Formula Tell Us?
- Some Common Questions About the Variance Formula
What is Variance and Why Do We Care?
Variance, at its heart, is a way to measure how much individual numbers in a collection tend to differ from the average number of that collection. It gives us a single figure that describes the general spread of all the numbers. Think of it this way: if you have a list of test scores, variance can tell you if most students scored very close to the class average, or if there was a wide range of scores, with some students doing very well and others struggling quite a bit. It is a statistical measurement that helps us figure out how much numbers in a data set spread out from the average value, or the mean.
Why do we care about this particular measurement? Well, it provides a deeper understanding of our information beyond just knowing the average. Knowing the average height of people in a town is one thing, but knowing the variance in heights tells you if most people are around that average, or if there are many very short people and many very tall people, with fewer in the middle. This kind of information is useful for making decisions. For example, a company looking at the consistency of a product might use variance to see if each item produced is very similar to the last, or if there is a lot of difference between them. So, it really helps to paint a more complete picture of the numbers we are looking at.
It's like looking at a group of people and wanting to know if they are all roughly the same age, or if there is a big mix of young children, teenagers, adults, and older folks. The variance formula helps us quantify that feeling of spread. It's a numerical value, and it helps to show how widely individuals in a group are spread out. A very small variance means the numbers are quite similar to each other, clustered around the average. A large variance, on the other hand, means the numbers are quite different from each other, stretching out over a wider range. This understanding is pretty important for making sense of many kinds of information, you know, whether it is about people, things, or events.
How Do We Think About the Variance Formula?
When we talk about the variance formula, we are really discussing the mathematical recipe for figuring out this measure of spread. It involves a few specific steps that take each individual number, compare it to the average, and then do some calculations with those differences. The goal is to get a single number that summarizes how much variation exists. This formula is a key tool in many fields where people work with numbers, because it helps them understand the consistency or inconsistency of what they are observing. In probability studies and statistics, the variance formula gives us a way to measure how far a set of numbers are spread out.
There are, in some respects, a couple of main ways to think about the variance formula, depending on whether you are looking at an entire group of things or just a smaller collection taken from a larger group. For instance, if you wanted to know the variance of all the trees in a specific forest, you would use one version of the formula. But if you only measured a small number of trees and wanted to estimate the variance of the entire forest from those few measurements, you would use a slightly different version. This distinction is quite important because it affects the accuracy of your spread estimate. The two kinds of variance are closely related, but the calculation does differ a little.
The core idea behind the variance formula is always the same, though. It's about looking at how much each individual piece of information moves away from the average of the whole group. We square these differences, which is a step that helps make sure that positive and negative differences do not cancel each other out, and it also gives more weight to numbers that are much further from the average. Then, we average these squared differences. This average of the squared differences from the mean is how variance is calculated. It's a rather clever way to get a single number that truly reflects the overall spread of your data. You can, for example, see how this method accounts for how far members are from the average, and it judges each observation's importance by this same distance.
Different Ways to Calculate the Variance Formula
The way you figure out the variance formula can change a little bit depending on the kind of information you are working with. For instance, if you have a simple list of individual numbers, where each number stands on its own, you use one approach. This is often called "ungrouped data." If your information is already sorted into categories or ranges, like a list showing how many people fall into certain age brackets, that is called "grouped data," and the formula for that looks a bit different. For ungrouped data, variance is found by taking the average of the squared differences, as a matter of fact.
When we are talking about an entire collection of things, like every single student in a school, we call that a "population." The variance formula for a population is slightly different from the one you would use if you only had a "sample," which is just a smaller selection of students from that school. The difference comes down to how you divide at the very end of the calculation. For a population, you divide by the total number of items. For a sample, you typically divide by one less than the total number of items, which helps to give a more accurate estimate of the spread of the larger group from which the sample was taken. This subtle change is quite important for getting the right estimate.
So, you see, there are multiple ways to figure out an estimate of the population variance, and these differences are worth noting. It is not just one single, rigid method that applies to every situation. Knowing whether your information is grouped or ungrouped, and whether it represents a full population or just a sample, helps you pick the right version of the variance formula. This ensures that the number you get for the spread is as accurate and meaningful as possible for your specific situation. This is why it's useful to write down the sample variance formula if that is what you are working with, for instance, to keep track of the correct method.
How Do You Work Out the Variance Formula by Hand?
If you want to figure out the variance formula for a set of numbers without using a computer program, you can certainly do it by hand. It involves a few clear steps. First, you need to find the average of all your numbers. This average, or mean, is the central point from which you will measure how much each number differs. Once you have that average, you take each individual number in your list and subtract the average from it. This gives you the difference, or deviation, of each number from the center. You know, it's pretty straightforward to begin with.
After you have found all those differences, the next step in working with the variance formula is to square each of those differences. Squaring means you multiply the number by itself. So, if a difference was 5, you would get 25. If a difference was -3, you would get 9. This squaring step is really important because it makes all the numbers positive, meaning that differences above the average and differences below the average both contribute positively to the overall measure of spread. It also gives more weight to numbers that are much further away from the average, which is rather useful for showing big variations. Repeat this process for all data points.
Once you have all the squared differences, you then add all of those squared values together. This sum represents the total amount of squared deviation from the average across your entire set of numbers. Finally, to complete the variance formula, you divide that total sum by the number of data points you have. If you are working with a sample, you typically divide by one less than the number of data points. This final division gives you the average of the squared differences, which is your variance. So, to find the variance, you take a data point, subtract the population mean, and square that difference. Then, sum all of those squared values and divide by the appropriate number.
What is the Connection Between Variance and Standard Deviation?
Variance and standard deviation are very closely related concepts, almost like two sides of the same coin when we are talking about how much numbers spread out. The standard deviation is, in fact, simply the square root of the variance. Think of it this way: the variance formula gives you a number that is in "squared units." For example, if you were measuring heights in inches, the variance would be in "square inches," which isn't very intuitive to think about in real-world terms. The standard deviation brings that measurement back into the original units, making it much easier to understand and use.
Because the standard deviation is expressed in the same units as your original data, it is often more commonly used to describe the spread. For instance, if the average height of a group is 65 inches and the standard deviation is 3 inches, you can easily picture that most people are likely to be within a few inches of 65. If you only had the variance, say 9 square inches, it would be harder to get that immediate sense of the spread. So, the standard deviation squared will give us the variance, and taking the square root of the variance gives us the standard deviation. This relationship is pretty fundamental in statistics, you know.
They both tell you the same thing about the spread of numbers, but they do it in slightly different ways. Variance gives you the average squared difference from the mean, which is great for mathematical calculations and for breaking down how different sources contribute to overall variation. Standard deviation, on the other hand, provides a more direct and easily interpretable measure of spread, because it is in the same units as the original data. So, while the variance formula is the basis for figuring out spread, the standard deviation is often the number that people use to actually talk about and understand that spread in everyday situations. They are both really important tools for looking at information sets.
Using a Tool for the Variance Formula
While figuring out the variance formula by hand is a good way to understand how it works, for larger sets of numbers, using a tool can save you a lot of time and effort. There are many online calculators and software programs that can do the calculations for you very quickly. These tools are designed to take your list of numbers and automatically apply the variance formula, giving you the result without you having to do all the individual subtractions, squares, and divisions. This is especially helpful when you have hundreds or even thousands of data points, which would be quite a lot to do by hand.
A good variance calculator will not just give you the final number for the variance. It will often also provide other related measurements that are useful for understanding your data. For example, many calculators will also show you the standard deviation, which, as we discussed, is directly related to variance and often easier to interpret. They might also tell you the total number of data points you entered, the mean (average) of your numbers, and even the sum of squares, which is one of the intermediate steps in the variance formula calculation. You can, for instance, see the work performed for the calculation on some of these tools.
Using a calculator or software for the variance formula also helps to avoid small arithmetic mistakes that can easily happen when doing many calculations by hand. It ensures accuracy and consistency in your results. So, while it's great to know the steps involved, don't hesitate to use these convenient tools when you are working with real-world information. They make the process much more efficient and reliable. It's really about making the task easier and more precise, you know, especially when dealing with a lot of numbers.
What Does a Number From the Variance Formula Tell Us?
Once you have a number from the variance formula, what does it actually mean? Well, this number is a direct indicator of how much your data points are spread out. A very small variance, or a number close to zero, tells you that all the individual numbers in your collection are quite similar to each other. They are clustered very tightly around the average. Think of a group of pencils that are all almost exactly the same length; their length variance would be very small. The closer the variance is to zero, the more closely the data points are gathered.
On the other hand, if you get a large number from the variance formula, it means that your data points are quite spread out from each other. There is a lot of difference between the individual numbers and the average. For example, if you looked at the ages of people at a family reunion, you would likely find a large variance because you would have very young children, teenagers, adults, and older relatives, all in one group. This wide range would result in a bigger variance number. The larger the variance, the more spread out the data is, as a matter of fact.
So, the variance of a data set tells you how spread out the data points are. It gives you a sense of the consistency or variability within your information. This is really useful for making comparisons. If you are comparing two different sets of numbers, the one with the smaller variance is more consistent, or less spread out. The one with the larger variance is more varied. This simple numerical value helps you get a quick sense of the overall pattern of your numbers, which is pretty helpful for drawing conclusions or making decisions about what you are observing. It's a key piece of information when you are trying to understand a collection of figures.
Some Common Questions About the Variance Formula
People often have questions about the variance formula, especially when they are just starting to learn about it. One common point of confusion is the difference between population variance and sample variance. As we touched on, the way you divide at the end of the calculation changes. For a population, you divide by the total count of items. For a sample, you divide by one less than the total count. This adjustment for samples is done to give a better estimate of the spread of the larger group from which the sample came. A phrase like "mean of squares minus the square of means" is a description of a formula for the population variance, not the sample variance, for example.
Another area where questions come up involves more advanced uses of the variance formula, such as when dealing with weighted averages or in more complex statistical models. For instance, sometimes you might need to calculate the variance of a prediction in a linear model, which can involve more complex matrix notation. There can be a surprising amount of confusion when it comes to unbiased weighted variance, for instance, even among those who work with numbers often. The core idea of spread remains the same, but the specific steps and formulas can get more involved depending on the situation. There appears to be a general agreement toward specific formulas for these more complex situations.
Sometimes, people also wonder how variance relates to other statistical concepts, like mean squared error (MSE) or different types of probability distributions. For example, the mean squared error can actually be broken down into variance plus the square of bias, which is a key idea in understanding the accuracy of estimates. Also, knowing the variance can help you determine if a certain type of probability distribution exists for a given set of conditions. These are more specialized applications, but they show how fundamental the variance formula is to many areas of working with numbers. It's pretty clear that this concept is widely used in many different statistical discussions.

Variance Calculator (with Steps) - Inch Calculator
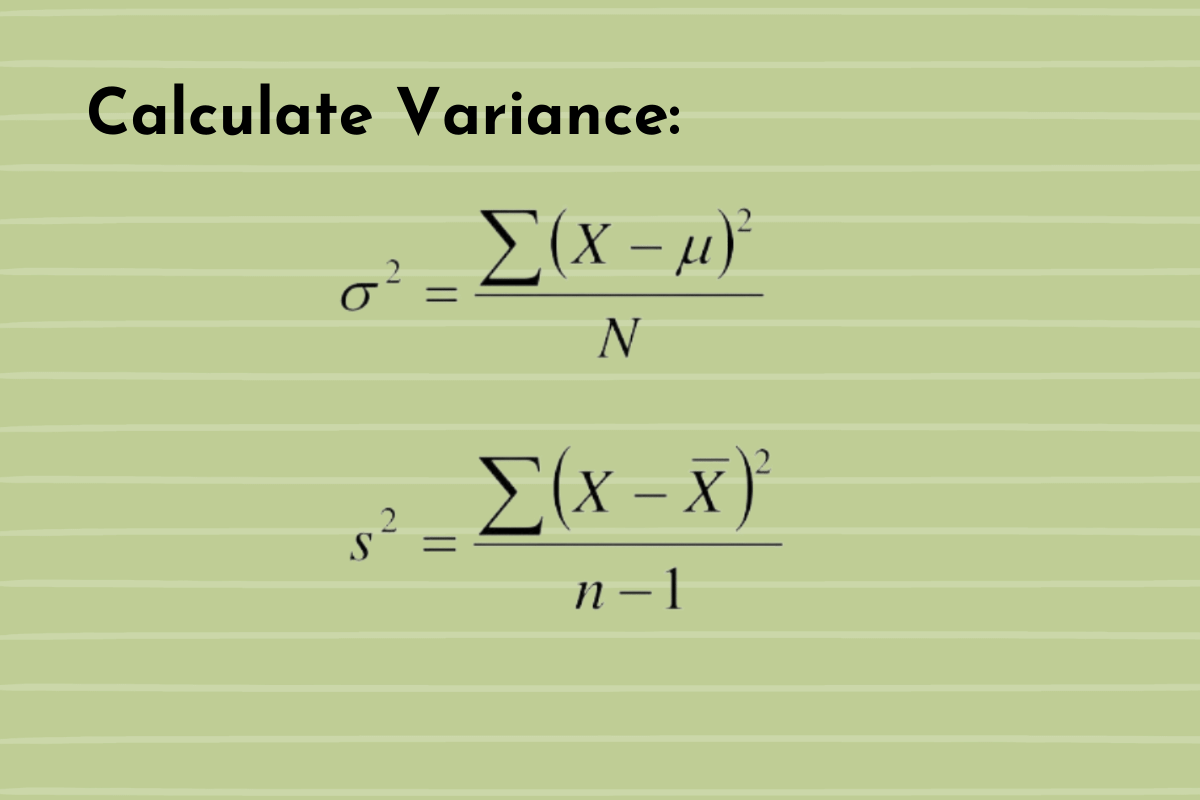
How to Calculate Variance | knowhowadda

Variance Formula